تفتاش جوجي (ألݣوريتم)
 مقالة زنقة ماكاتخرجش. هاد لمقالة زنقة ما كاتخرجش، ما كاتوصّل ل تا شي مقالة خرة، حاول تزيد فيها ليانات د مقالات خرين كاينين ف لموسوعة. مقالة زنقة ماكاتخرجش. هاد لمقالة زنقة ما كاتخرجش، ما كاتوصّل ل تا شي مقالة خرة، حاول تزيد فيها ليانات د مقالات خرين كاينين ف لموسوعة.ماتّخلعش! هاد لميصاج مديور باش تشوفو لفرقة ديال الصيانة و لمراجعة د لمقالات، و ماكيعنيش بلي درتي شي غلط! |
| لمقال مقطوع من شجرة، ما كايدي ليه تا شي مقال أخر، زيد ليان ديالو ف مقالات خرين. |
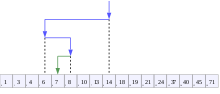 متال ديال تطبيق د لألݣوريتم فين لعنصر لهدف هو 7 | |
| كلاص | ألݣوريتم د تفتاش |
|---|---|
| قلدة د الداطا | ليستة |
| تعقيد د لوقت ف أكفس حالة | |
| تعقيد د لوقت ف أحسن حالة | |
| تعقيد د لوقت ف لحالة لمتوسطة | |
| تعقيد د لميموار ف لحالة لمتوسطة | |
ف لانفورماتيك، تّفتاش جّوجي ( بلينݣليزية Binary search ː ) هو ألݣوريتم د تفتاش. كتستعمل ماش تجبر موطاع ديال شي عنصر هدف ف شي ليستة مستفة. تفتاش جوجي كيقارن ديك لعنصر لهدف مع لعنصر لي جا فلوصط ديال ليستة، إدا كانو قد قد سالينا، و إلا كان لهدف صغير من لوصط، كيفتّش ف نص د شْمال (ليستة مستفة من صغير ن لكبير من شمال ن ليمن) د ليستة، إلا كان لهدف كبير من لوصط كيفتش ف نص د ليمن د ليستة. بهاد طريقة طاية ديال ليستة كتقسم على جوج ف كل دورة ديال لألݣوريتم. هنا من جا لإسم ديالو.
تعقيد ف لوقت ديالو هو فين هو طاي د ليستة.[1] تّفتاش جّوجي سرع من تفتاش لخطي (تعقيد ف لوقت ديالو ) من غير بنسبة ن ليستات قصارين. ولكن لّيستة خاص ضروري تكون مستفة ماش يتطبق هاد لألݣوريتم بينما تّفتاش لخطي كيخدم فجميع لحالات.
لكود ف پايطون
بدلهادا متال ديال لألݣوريتم ف پايطون، هنايا L هي ليستة، target هو لعنصر لهدف. هاد فونكسيون كترجع رقم تستافي ديال لهدف. ليستة مستفة من شمال ن ليمن (رقم تستافي لول هو 0 و لاخر هو طاي د L ناقص واحد). ادا لهدف مكانش ف ليستة كترجع 1-.
def binary_search(L, target):
l, r = 0, len(L)-1
while l <= r:
mid = (l+r)//2
if L[mid] == target:
return mid
elif L[mid] > target:
r = mid - 1
else:
l = mid + 1
return -1
تطبيق مسكسف
بدللحساب د بتفتاش جوجي
بدلعدد ماشي جدري، يعني ميمكنشي نكتبوه على شكل معا ولاكين يمكنا نقربولو بشحال ما بغينا و نجبرو تقريب ديالو على شكل عداد بلفاصلة.
أنسمّيو تّقريب ديال بدقة ديال يعني . عارفين بلي فهاد لحالة ليستة لمستفة هي ولعنصر الهدف هو .
def sqrt(y, epsilon):
l, r = 0, y
mid = (l+r)/2
while abs(mid**2-y) > epsilon:
mid = (l+r)/2
if mid**2 > y:
r = mid
elif mid **2 < y:
l = mid
return mid
ف پايطون ما يمكناشي نفوتو دقة ديال تقريبا.
عيون لكلام
بدل- ^ "Binary Search - Data Structure and Algorithm Tutorials". GeeksforGeeks (ب نڭليزية). 2014-01-28. مأرشيڤي من لأصل ف 2023-10-26. تطّالع عليه ب تاريخ 2023-10-26.
هادي زريعة ديال مقالة خاصها تّوسع. تقدر تشارك ف لكتبة ديالها. |



